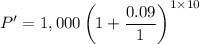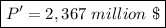Answer:
P'=2,367 million $
Explanation:
Compound Interest
It refers to the case where the interests earned in a certain period are added to the principal sum of a loan and re-invested. Interest in the next period is then earned on the principal sum plus previously accumulated interest.
Being P the principal, or initial amount of a loan or deposit, r the nominal annuual interest rate and t the time the interest is applied, the total accumlated value or future value is

According to the conditions of the problem, Christopher deposited 1 billion into his savings. This gives us the principal P=1,000 milion dollars. The interest rate is 9% compounded once a year during t=10 years. Here n=1 since the compounding does not occur in the middle of the yearly period. Thus