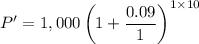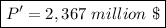Question

Christopher deposited 1 billion into his savings. His savings is a compound interest account with a rate of 9% and only compound once a year. How much money would Christopher have at the end of 10 years in millions?

Answer 1

your answer would B

Explanation:

Answer 2

P'=2,367 million $

Explanation:

Compound Interest

It refers to the case where the interests earned in a certain period are added to the principal sum of a loan and re-invested. Interest in the next period is then earned on the principal sum plus previously accumulated interest.

Being P the principal, or initial amount of a loan or deposit, r the nominal annuual interest rate and t the time the interest is applied, the total accumlated value or future value is

`{\displaystyle P'=P\left(1+{\frac {r}{n}}\right)^(nt)}`

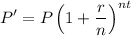
According to the conditions of the problem, Christopher deposited 1 billion into his savings. This gives us the principal P=1,000 milion dollars. The interest rate is 9% compounded once a year during t=10 years. Here n=1 since the compounding does not occur in the middle of the yearly period. Thus

`{\displaystyle P'=1,000\left(1+{\frac {0.09}{1}}\right)^(1* 10)}`

`\boxed{P'=2,367\ million\ \$}`