Question

find the present value of an investment that is worth $19,513.75 after earning 3percent simple interest for 5.5 years

Answer 1

present value = $16750

Explanation:

The simple interest formula allows us to calculate A, which is the final amount. According to this formula, the amount is given by A = P (1 + r*t), where P is the principal, r is the annual interest rate in decimal form, and t is the loan period expressed in years

simple interest formula:

t: time

P: present value

A: amount

r : anual interest

A = P (1 + r*t)

P = A / (1 + r*t)

P = 19,513.75 / (1 + 3/100 * 5.5)

P = 19,513.75/ (1 + 0.165)

P = 19,513.75 / 1.165

P = 16750

present value = $16750

Answer 2

The present value of the investment is $16750 after 5.5 years

Let A represent the value of the investment after 5.5 years, P represent the present value of the investment, I represent the interest, R represent the interest rate, T represent the time taken.

Given that A = $19513.75, R = 3% = 0.03, T = 5.5 years.

`I=PRT\\\\I=P*0.03*5.5\\\\I=0.165P`

`A=I+P\\\\A=0.165P+P\\\\A=1.165P\\\\19513.75=1.165P\\\\P=\$16750`

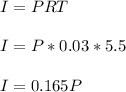
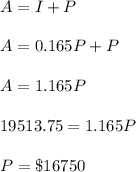
Therefore the present value of the investment is $16750