Question

What is the half-life of bismuth-214 if 34.7 minutes are required for the mass of a sample of bismuth-214 to fall to 29.5 percent of its original value? Since the decomposition is a radioactive decay reaction, it is first order.

Answer 1

The half life of bismuth-214 is 19.7 minutes.

Step-by-step explanation:

If 29.5% of bismuth-214 original value is remaining, then it means

`(N)/(N_0) = 0.295`

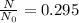
Also, In first-­order reaction; the rate of radioactive decay is proportional to the number of each type of radioactive nuclei present in a given sample.

`N = N_0e^(-\lambda t)`

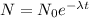
This equation gives us the number of radioactive nuclei present at time 't'

Where;

λ is decay constant and

t is the time of decay

Thus, the fraction of radioactive nuclei present at time 34.7 minutes is 0.295

`0.295 =e^(-\lambda t)`

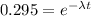
ln(0.295) = -λt

-1.2208 = -λt

λ = (1.2208)/(34.7 mins) = 0.03518/mins

Also,

`t_(1/2) =(0.693)/(\lambda) = (0.693)/(0.03518) = 19.7 mins`

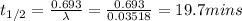
Therefore, the half life of bismuth-214 is 19.7 minutes.