Answer:
The half life of bismuth-214 is 19.7 minutes.
Step-by-step explanation:
If 29.5% of bismuth-214 original value is remaining, then it means
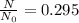
Also, In first-order reaction; the rate of radioactive decay is proportional to the number of each type of radioactive nuclei present in a given sample.
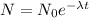
This equation gives us the number of radioactive nuclei present at time 't'
Where;
λ is decay constant and
t is the time of decay
Thus, the fraction of radioactive nuclei present at time 34.7 minutes is 0.295
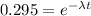
ln(0.295) = -λt
-1.2208 = -λt
λ = (1.2208)/(34.7 mins) = 0.03518/mins
Also,
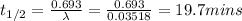
Therefore, the half life of bismuth-214 is 19.7 minutes.