Question

Anjeli writes the equation (a+b)2=c2+4(12ab) to begin a proof of the Pythagorean theorem.

Use the drop-down menus to explain why this is a true equation.

Answer 1

Therefore Anjeli is correct and

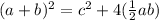`(a+b)^(2)=c^(2)+4((1)/(2)ab)` is TRUE.

Explanation:

Given:

Label on triangle as ΔABC right angle at C such that

AB = c .....(Hypotenuse)

AC = b ....(Longer leg)

BC = a ....(Shorter leg)

To Prove:

`(a+b)^(2)=c^(2)+4((1)/(2)ab)`

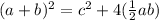
Proof:

We know, in Right angle triangle ABC by Pythagoras theorem we get,

`(\textrm{Hypotenuse})^(2) = (\textrm{Shorter leg})^(2)+(\textrm{Longer leg})^(2)`

Substituting the values we get

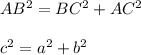`AB^(2)=BC^(2)+AC^(2)\\\\c^(2)=a^(2)+b^(2)` ...............( 1 )

Now the Left hand side of what Anjeli wrote is

Left hand side = (a+b)²

Using identity (A+B)² = A²+ B² + 2AB we get

Left hand side = a²+ b² + 2ab

From ( 1 ) we have
`c^(2)=a^(2)+b^(2)`

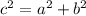
Substituting we get

Left hand side = c² + 2ab ...........................( 2 )

Now,

Right hand side =
`c^(2)+4((1)/(2)ab)`

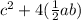
Dividing 4 by 2 we get 2, hence

Right hand side =
`c^(2)+2ab` .........................( 3 )

Therefore,

Left hand side = Right hand side From ( 2 ) and ( 3 )

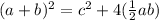`(a+b)^(2)=c^(2)+4((1)/(2)ab)` ..True

Therefore Anjeli is correct and

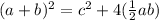`(a+b)^(2)=c^(2)+4((1)/(2)ab)` is TRUE.