Question

The combined area of two squares is 80 square centimeters. Each side of one square is twice as long as a side of the other square. What is the length of each side of the larger square?

Answer 1

The length of each side of the larger square is 8 centimeter.

Explanation:

Given:

The combined area of two squares is 80 square centimeters. Each side of one square is twice as long as a side of the other square.

Now, to find the length of each side of the larger square.

Let
`s` be the length of the smaller square.

So, the length of the larger square =
`2s.`

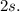
Now, we find the areas of the square by putting formula:

The area of smaller square = length²
`=s^2.`

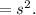
The area of larger square = (length)²
`=(2s)^2=4s^2.`

As, given:

The combined area of two squares is 80 square centimeters.

According to question:

`s^2+4s^2=80\\5s^2=80`

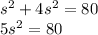
So, dividing both sides by 5 we get:

`s^2=16`

Using square root on both sides we get:

`s=4\ centimeter.`

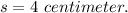
And, to get the length of each side of the larger square we substitute the value of
`s`:

`2s=2* 4=8\ centimeter.`

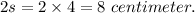
The length of larger square = 8 centimeter

Therefore, the length of each side of the larger square is 8 centimeter.