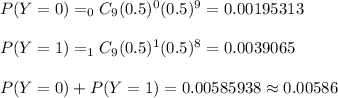Question

United Airlines' flights from Denver to Seattle are on time 50 % of the time. Suppose 9 flights are randomly selected, and the number on-time flights is recorded.

Answer 1

a) The probability that exactly 4 flights are on time is equal to 0.0313

b) The probability that at most 3 flights are on time is equal to 0.0293

c) The probability that at least 8 flights are on time is equal to 0.00586

Explanation:

The question posted is incomplete. This is the complete question:

United Airlines' flights from Denver to Seattle are on time 50 % of the time. Suppose 9 flights are randomly selected, and the number on-time flights is recorded. Round answers to 3 significant figures.

a) The probability that exactly 4 flights are on time is =

b) The probability that at most 3 flights are on time is =

c)The probability that at least 8 flights are on time is =

Solution to the problem

a) Probability that exactly 4 flights are on time

Since there are two possible outcomes, being on time or not being on time, whose probabilities do not change, this is a binomial experiment.

The probability of success (being on time) is p = 0.5.

The probability of fail (note being on time) is q = 1 -p = 1 - 0.5 = 0.5.

You need to find the probability of exactly 4 success on 9 trials: X = 4, n = 9.

The general equation to find the probability of x success in n trials is:

`P(X=x)=_nC_x\cdot p^x\cdot (1-p)^((n-x))`

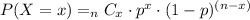
Where
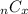`_nC_x` is the number of different combinations of x success in n trials.

`_nC_x=(x!)/(n!(n-x)!)`

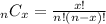
Hence,

`P(X=4)=_9C_4\cdot (0.5)^4\cdot (0.5)^(5)`

`_9C_4=(4!)/(9!(9-4)!)=126`

`P(X=4)=126\cdot (0.5)^4\cdot (0.5)^(5)=0.03125`

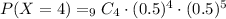
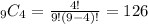
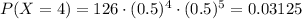
b) Probability that at most 3 flights are on time

The probability that at most 3 flights are on time is equal to the probabiity that exactly 0 or exactly 1 or exactly 2 or exactly 3 are on time:

`P(X\leq 3)=P(X=0)+P(X=1)+P(X=2)+P(X=3)`

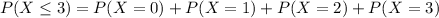
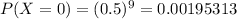`P(X=0)=(0.5)^9=0.00195313` . . . (the probability that all are not on time)

`P(X=1)=_9C_1(0.5)^1(0.5)^8=9(0.5)^1(0.5)^8=0.00390625`

`P(X=2)=_9C_2(0.5)^2(0.5)^7=36(0.5)^2(0.5)^7=0.0078125`

`P(X=3)= _9C_3(0.5)^3(0.5)^6=84(0.5)^3(0.5)^6=0.015625`

`P(X\leq 3)=0.00195313+0.00390625+0.0078125+0.015625=0.02929688\\\\ P(X\leq 3) \approx 0.0293`

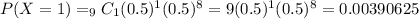
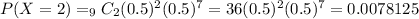
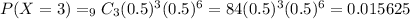
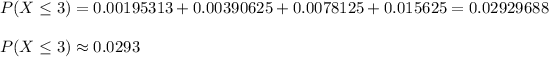
c) Probability that at least 8 flights are on time

That at least 8 flights are on time is the same that at most 1 is not on time.

That is, 1 or 0 flights are not on time.

Then, it is easier to change the successful event to not being on time, so I will change the name of the variable to Y.

`P(Y=0)=_0C_9(0.5)^0(0.5)^9=0.00195313\\ \\ P(Y=1)=_1C_9(0.5)^1(0.5)^8=0.0039065\\ \\ P(Y=0)+P(Y=1)=0.00585938\approx 0.00586`