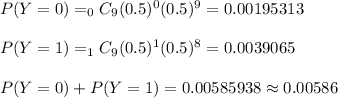Answer:
a) The probability that exactly 4 flights are on time is equal to 0.0313
b) The probability that at most 3 flights are on time is equal to 0.0293
c) The probability that at least 8 flights are on time is equal to 0.00586
Explanation:
The question posted is incomplete. This is the complete question:
United Airlines' flights from Denver to Seattle are on time 50 % of the time. Suppose 9 flights are randomly selected, and the number on-time flights is recorded. Round answers to 3 significant figures.
a) The probability that exactly 4 flights are on time is =
b) The probability that at most 3 flights are on time is =
c)The probability that at least 8 flights are on time is =
Solution to the problem
a) Probability that exactly 4 flights are on time
Since there are two possible outcomes, being on time or not being on time, whose probabilities do not change, this is a binomial experiment.
The probability of success (being on time) is p = 0.5.
The probability of fail (note being on time) is q = 1 -p = 1 - 0.5 = 0.5.
You need to find the probability of exactly 4 success on 9 trials: X = 4, n = 9.
The general equation to find the probability of x success in n trials is:
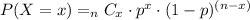
Where
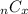 is the number of different combinations of x success in n trials.
is the number of different combinations of x success in n trials.
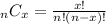
Hence,

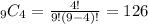
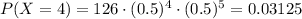
b) Probability that at most 3 flights are on time
The probability that at most 3 flights are on time is equal to the probabiity that exactly 0 or exactly 1 or exactly 2 or exactly 3 are on time:
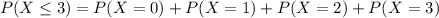
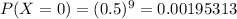 . . . (the probability that all are not on time)
. . . (the probability that all are not on time)

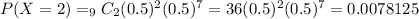
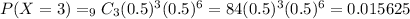
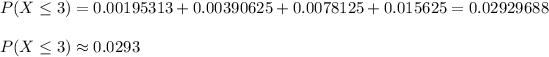
c) Probability that at least 8 flights are on time
That at least 8 flights are on time is the same that at most 1 is not on time.
That is, 1 or 0 flights are not on time.
Then, it is easier to change the successful event to not being on time, so I will change the name of the variable to Y.