Answer:
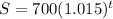
It will take 36.2 years.
Explanation:
The principal amount is $700. This principal amount earns 1.5% interest that is compounded annually.
Therefore, from the formula of compound interest, we can write
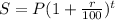 , where S is the maturity sum and P is the principal invested and r% is the interest which is compounded annually and t is the number of years.
, where S is the maturity sum and P is the principal invested and r% is the interest which is compounded annually and t is the number of years.
So, in our case, the equation will be
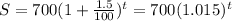 ............ (1) (Answer)
............ (1) (Answer)
Now, if the maturity sum, S = $1200, then,
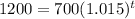
⇒
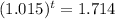
Now, taking log both sides,
t(log 1.015) = log 1.714
⇒ t = 36.2 years.