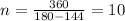Answer:
x =
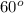
number of sides of each polygon = 10
Explanation:
The first thing you need to know while solving these problems are the following formulas:
Sum of interior angles of a polygon, S =
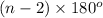
where n = number of sides
and for a regular polygon, each angle =
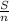
For example, a triangle has 3 sides and the sum of it's interior angles =
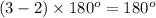 and each angle of an equilateral triangle =
and each angle of an equilateral triangle =
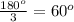
Now, for a regular hexagon (first problem), each interior angle =
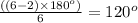
which is also the larger angle of the rhombus.
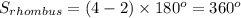
Therefore, the smaller angle of the rhombus =
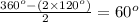
From which we get the value of x =
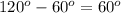
Congruent polygons have the same number sides and the corresponding sides and interior angles will be equal.
In the figure (second problem), we are given two congruent regular polygons which means that both polygons will have equal interior angles.
Now, we know that the total angle about a point =
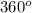
Let the interior angles of the polygons be denoted by
 .
.
Therefore,
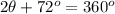
or,
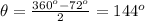
From the first two formulas, we can say that,
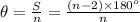
or,
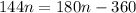
or,