Question

Complete the recursive formula of the geometric sequence −0.1 ,−0.5 ,−2.5 ,−12.5

c(1)=______
c(n)=c(n-1)*______

Answer 1

First answer = -0.1

Second answer = 5

Answer 2

c(1)=-0.1

c(n)=c(n-1)*5

Explanation:

The recursive definition of a geometric sequence is given by:

`c(n) = c(n - 1) * r`

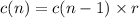
where r is the common ratio.

The given given geometric sequence is −0.1 ,−0.5 ,−2.5 ,−12.5

c(1) is the first term.

This implies that:

c(1)=-0.1

To find the common ratio, we divide the subsequent terms of any two consecutive term by the previous term

`r = ( - 0.5)/( - 0.1) = 5`

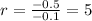
The recursive formula is

c(1)=-0.1

c(n)=c(n-1)*5