Question

Hello, could anyone please help me with my homework?

My question is:-
(x+6)^6
Please solve A.S.A.P.
Kindly don't lose your precious time by spamming; instead, please provide a high-quality answer. Thanks in advance :-)

Answer 1

`(x + 6 {)}^(6) = {x}^(6 ) + 36{x}^(5) + 540{x}^(4) + 4320 {x}^(3) + 19440{x}^(2)+ 46656{x}^{} + 46656`

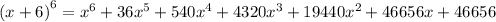
Explanation:

we want to solve the following binomial:

`(x + 6 {)}^(6)`

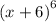
There is a handy way to expand powers of binomials which is known as binomial theorem . and it describes the algebraic expansion of powers of a binomial. binomial theorem is given by

`\displaystyle (a + b {)}^(n) = \sum _(k = 0 )^(n) \binom{n}{k} {a}^(n - k) {b}^(k)`

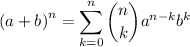
comparing (x+6)⁶ to (a+b)ⁿ , we get

• 
  `a \implies \: x`
• 
  `b\implies \: 6`
• 
  `n\implies \: 6`

now substitute them on the formula which yields:

`\displaystyle (x + 6 {)}^(6) = \sum _(k = 0 )^(n) \binom{6}{k} {x}^(6 - k) \cdot {6}^(k)`

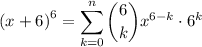
converting the summation notation into sum yields:

`\displaystyle (x + 6 {)}^(6) = \binom{6}{0} {x}^(6 - 0) \cdot {6}^(0) + \binom{6}{1} {x}^(6 - 1) \cdot {6}^(1) + \binom{6}{2} {x}^(6 - 2) \cdot {6}^(2) + \binom{6}{3} {x}^(6 - 3) \cdot {6}^(3) + \binom{6}{4} {x}^(6 - 4) \cdot {6}^(4) + \binom{6}{5} {x}^(6 - 5) \cdot {6}^(5) + \binom{6}{6} {x}^(6 - 6) \cdot {6}^(6) \\ \implies(x + 6 {)}^(6) = \binom{6}{0} {x}^(6 ) \cdot 1 + \binom{6}{1} {x}^(5) \cdot {6} + \binom{6}{2} {x}^(4) \cdot 36+ \binom{6}{3} {x}^(3) \cdot 216 + \binom{6}{4} {x}^(2) \cdot 1296+ \binom{6}{5} {x}^{} \cdot 7776+ \binom{6}{6} {x}^(0) \cdot 46656 \\ \implies(x + 6 {)}^(6) = 1 \cdot {x}^(6 ) \cdot 1 + 6 \cdot{x}^(5) \cdot {6} + 15 \cdot {x}^(4) \cdot 36+ 20 \cdot {x}^(3) \cdot 216 + 15 \cdot{x}^(2) \cdot 1296+ 6 \cdot {x}^{} \cdot 7776+ 1 \cdot {x}^(0) \cdot 46656 \\ \implies \boxed{ (x + 6 {)}^(6) = {x}^(6 ) + 36{x}^(5) + 540{x}^(4) + 4320 {x}^(3) + 19440{x}^(2)+ 46656 {x}^{} + 46656 }`

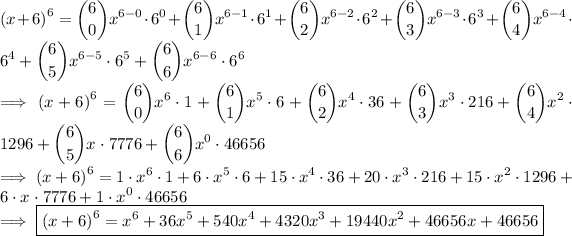
and we're done!