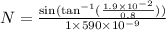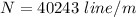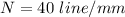Answer:B
Step-by-step explanation:
Given
Wavelength of light
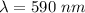
Screen distance
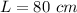
First fringe is at a distance
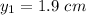
No of lines per mm is given by N
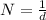
where d=slit width
From N-slits Experiment
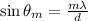

Position of bright fringe is given by
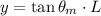
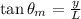
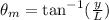
Put the value of
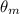 in eq. 1
in eq. 1
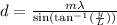
Therefore

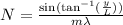
for