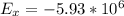Answer:
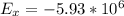
Explanation:
Parameters given:
Point charge at the center of the sphere,
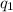 :
:
 μC
μC
Charge of the sphere,
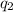 :
:
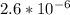 μC
μC
Distance between
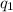 and the point of consideration =
and the point of consideration =

Distance between
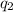 and the point of consideration =
and the point of consideration =

Electric field is given as
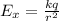
where
k = Coulombs constant;
q = electric charge;
r = distance between charge and point of consideration.
The net electric field at that point is the sum of the electric field due to
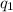 and
and
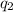 , i.e.:
, i.e.:

Since k is the same and the distance, r is also the same, then:
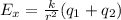
=>
![E_x =(9 * 10^9)/((8.8 * 10^(-2))^2) [ (-7.7 * 10^(-6)) + (2.6 * 10^(-6))]](https://img.qammunity.org/2021/formulas/mathematics/college/3foiv4yhag4nj8i3zjd3cfch0102ia2rcu.png)
=>
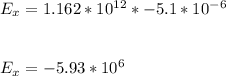
The electric field along the x axis,