Question

VERY EASY PLZ ANSWER.....Robert and Tony love to read. Robert reads 30 pages on the first day and 20 pages each day after that. Tony reads 40 pages on the first day and 15 pages each day after that. Which graph represents the total number of pages each has read after each day?

Answer 1

It's B.

Step-by-step explanation:

Took the same test!!!

Answer 2

• The first graph (see figure attached)

Step-by-step explanation:

1. Number of pages read by Robert

Set a function for the number of pages read by Robert, taking into account that this is an arithmetic sequence, whose first term is 30, and the common difference is 20:

`a_n=a_0+d(n-1)`

• R(n) = 30 + 20 (n - 1)

↑ ↑ ↑

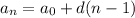
first day next days

2. Number of pages read by Tony:

The arithmetic sequence that represents the number of pages read by Tony has first term 40, and common difference 14:

`a_n=a_0+d(n-1)`

• T(n) = 40 + 15 (n - 1)

↑ ↑ ↑

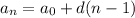
first day next days

3. Find the numbers of pages read by Tony in terms of the number of pages read by Robert.

To do that, you must clear n from both equations and equal the two expressions obtained:

From R(n) = 30 + 20 (n - 1):

• R(n) = 30 + 20n - 20
• R(n) = 10 + 20n
• n = [R(n) - 10]/20

You can change R(n) to r:

• n = (r - 10) / 20

From T(n) = 40 + 15 (n - 1)

• T(n) = 40 + 15n - 15

• T(n) = 25 + 15n

• n = [T(n) - 25]/15

Change T(n) to t

• n = (t - 25)/15

Equal both expressions:

• (r - 10) / 20 = (t - 25)/15

Solve for t:

• 15(r-10) = 20(t - 25)

• 15r - 150 = 20t - 500

• 15r - 150 + 500 = 20t

• 15r + 350 = 20t

• 3r + 70 = 4t

• 4t = 3r + 70

• t = (3/4)r + 70/4

• t = 0.75r + 17.5

Find some points of the equation t = 0.75r - 17.5 to compare with the points of the graph:

• r = 0 ⇒ t = 17.5, that means that the line intercepts the vertical axis at 17.5. The only graph that matches this is the first graph

Find other point:

• r = 30 ⇒ t = 0.75(30) + 17.5 = 40.Thus, the graph must contain the point (30, 40), which the first graph does.