We are given the equation of circle (x - 2)² + (y + 11)² = 100 , but let's recall the standard equation of circle i.e (x - h)² + (y - k)² = r², where (h, k) is the centre of the circle and r being the radius ;
So, consider the equation of circle ;
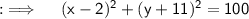
Can be further written as ;
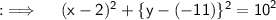
On comparing this equation with the standard equation of Circle, we will get, centre and radius as follows
- Centre = (2, -11)
- Radius = 10 units