Answers are in bold
S1 = 1
S2 = 0.5
S3 = 0.6667
S4 = 0.625
S5 = 0.6333
=========================================================
Step-by-step explanation:
Let
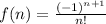
The summation given to us represents the following
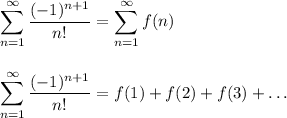
There are infinitely many terms to be added.
-------------------
The partial sums only care about adding a finite amount of terms.
The partial sum
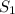 is the sum of the first term and nothing else. Technically it's not really a sum because it doesn't have any other thing to add to. So we simply say
is the sum of the first term and nothing else. Technically it's not really a sum because it doesn't have any other thing to add to. So we simply say
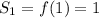
I'm skipping the steps to compute f(1) since you already have done so.
-------------------
The second partial sum is when things get a bit more interesting.
We add the first two terms.
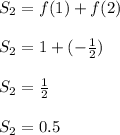
The scratch work for computing f(2) is shown in the diagram below.
-------------------
We do the same type of steps for the third partial sum.

The scratch work for computing f(3) is shown in the diagram below.
-------------------
Now add the first four terms to get the fourth partial sum.
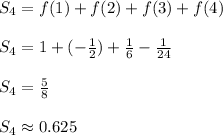
As before, the scratch work for f(4) is shown below.
I'm sure you can notice by now, but the partial sums are recursive. Each new partial sum builds upon what is already added up so far.
This means something like
 and
and
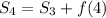
In general,
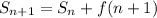 so you don't have to add up all the first n terms. Simply add the last term to the previous partial sum.
so you don't have to add up all the first n terms. Simply add the last term to the previous partial sum.
-------------------
Let's use that recursive trick to find
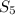
![S_5 = [f(1)+f(2)+f(3)+f(4)]+f(5)\\\\S_5 = S_4 + f(5)\\\\S_5 = (5)/(8) + (1)/(120)\\\\S_5 = (19)/(30)\\\\S_5 \approx 0.6333](https://img.qammunity.org/2023/formulas/mathematics/college/k3fkt2t6bhxs89hqilwgk71yqzk09lfeoi.png)
The scratch work for f(5) is shown below.