To avoid any ambiguity; the correct question is given as;
Hydrogen iodide decomposes according to the reaction 2 HI(g) ⇔ H₂ (g) + I₂ (g) A sealed 1.50 - L container initially holds 0.00623 mol of H₂, 0.00414 mol of I₂, and 0.0244 mol of HI at 703 K. When equilibrium is reached, the concentration of H₂(g) is 0.00467 M. What are the concentrations of HI(g) and I₂(g)?
Answer:
the concentrations of HI(g) and I₂ (g) are 0.01526 M and 0.00052 M respectively.
Step-by-step explanation:
Given that;
the number of moles of H₂ = 0.00623 mol
the number of moles of I₂ = 0.00414 mol
the number of moles of HI = 0.0244 mol; &
The volume of the sealed container = 1.50 - L
the concentration of H₂(g) is 0.00467 M when the equilibrium is reached.
We can determine their corresponding Molarity;
Since Molarity =
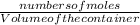
∴ Moiarity of H₂ =
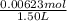
= 0.00415 M
Moiarity of I₂ =
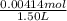
= 0.00276 M
Moiarity of HI =
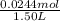
= 0.0163 M
Using the ICE table for the equation of the reaction, we have the following illustration as shown below;
2 HI(g) ⇔ H₂ (g) + I₂ (g)
Initial 0.0163 M 0.00415 M 0.00276 M
Change - 2x +x +x
Equilibrium (0.0163 - 2x) (0.00415+x) (0.00276+x)
Let's not forget that from our parameters given, it is stated that " the concentration of H₂(g) is 0.00467 M when the equilibrium is reached"
Therefore, if we relate the given equilibrium concentration with the equilibrium concentration from the ICE table; we have:
(0.00415+x) = 0.00467
x = 0.00467 - 0.00415
x = 0.00052 M
Since x = 0.00052 M, we can calculate our concentration of HI (g) and I₂(g)
The concentration of HI (g) = 0.0163 - 2x
where; x = 0.00052
∴ The concentration of HI (g) = 0.0163 - 2(0.00052)
= 0.01526 M
The concentration of I₂(g) = 0.00276+x
where; x = 0.00052
∴ The concentration of I₂(g) = 0.00276 + 0.00052
= 0.00328 M
Hence, the concentration of HI(g) and I₂ (g) are 0.01526 M and 0.00052 M respectively.