Question

A CI is desired for the true average stray-load loss μ (watts) for a certain type of induction motor when the line current is held at 10 amps for a speed of 1500 rpm. Assume that stray-load loss is normally distributed with σ = 3.19. (Round your answers to two decimal places. You must enter the LOWER BOUND first then the UPPER BOUND second.) (a) Compute a 95% CI for μ when n = 25 and x = 54.34.

Answer 1

`54.34 - 1.96 (3.19)/(√(25))=53.09`

`54.34 + 1.96 (3.19)/(√(25))=55.59`

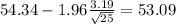
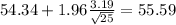
The 95% confidence interval is given by (53.09;55.59)

Explanation:

Normal distribution, is a "probability distribution that is symmetric about the mean, showing that data near the mean are more frequent in occurrence than data far from the mean".

The confidence interval is given by this formula:

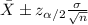`\bar X \pm z_(\alpha/2) (\sigma)/(√(n))` (1)

And for a 95% of confidence the significance is given by
`\alpha=1-0.95=0.05`, and
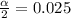`(\alpha)/(2)=0.025`. Since we know the population standard deviation we can calculate the critical value
`z_(0.025)= \pm 1.96`

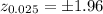
Confidence interval

`n=25,\bar X=54.34,\sigma=3.19`

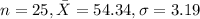
If we use the formula (1) and we replace the values we got:

`54.34 - 1.96 (3.19)/(√(25))=53.09`

`54.34 + 1.96 (3.19)/(√(25))=55.59`

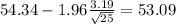
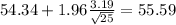
The 95% confidence interval is given by (53.09;55.59)