Question

A circle is shown. A secant and a tangent intersect at a common point outside of the circle to form an angle that measure 51 degrees. The measure of the first arc formed is x degrees and the measure of the second arc formed is 160 degrees. What is the value of x? x =

Answer 1

58

Explanation:

Answer 2

The value of x is 58°.

Solution:

The measure of the first arc formed = x°

The measure of the second arc formed = 160°

Angle formed between tangent and secant = 51°

Theorem:

If a secant and a tangent intersect at a common point in the exterior of a circle, then the measure of the angle formed is the half the difference of the measures of the intercepted arcs.

`$\Rightarrow 51^(\circ)=(1)/(2)(160^(\circ) -x^(\circ))`

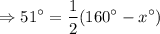
Multiply by 2 on both sides of the equation.

`$\Rightarrow 51^(\circ)* 2=2*(1)/(2)(160^(\circ) -x^(\circ))`

`$\Rightarrow 102^(\circ)=160^(\circ) -x^(\circ)`

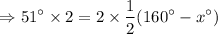
Subtract 160° on both sides of the equation.

`$\Rightarrow 102^(\circ)-160^(\circ)=160^(\circ) -x^(\circ)-160^(\circ)`

`$\Rightarrow -58^(\circ)=-x^(\circ)`

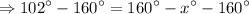
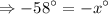
Multiply by (–1) on both sides of the equation.

`$\Rightarrow -58^(\circ)*(-1)=-x^(\circ)*(-1)`

`$\Rightarrow x^(\circ)=58^(\circ)`

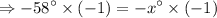
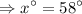
Hence the value of x is 58°.