The volume of globe is 381.51 cubic inches when the dimensions of the globe were reduced by half
Solution:
The globe is usually of spherical shape
The volume of sphere is given as:
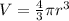
Where, "r" is the radius of sphere
Given that diameter is 18 inches
Diameter = 18 inches
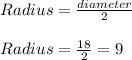
Thus radius is 9 inches
The dimensions of the globe were reduced by half
Thus radius is reduced by half
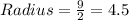
Now find the volume of sphere
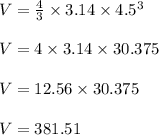
Thus volume of globe is 381.51 cubic inches