Question

A newspaper reported the results of a survey on the planning habits of men and women. In response to the question​ "What is your preferred method of planning and keeping track of​ meetings, appointments, and​ deadlines?" 54​% of the men and 44​% of the women answered​ "I keep them in my​ head." A nationally representative sample of​ 1,000 adults participated in the​ survey; therefore, assume that 500 were men and 500 were women. Complete parts 1 through 5.1. Set up the null and alternative hypotheses for testing whether the percentage of men who prefer keeping track of appointments in their head, p_1, is larger than the corresponding percentage of women, p_2. Choose the correct answer below. a. H_0: p_1 - p_2 = 0 versus H_a: p_1 - p_2 < 0 b. H_0: p_1 - p_2 = 0 versus H_a: p_1 - p_2 ≠ 0 c. H_0: p_1 - p_2 = 0 versus H_1: p_1 - p_2 > 02. Compute the test statistic for the test.3. Give the rejection region for the test, using α = 0.104. Find the p-value for the test.5. Make an appropriate conclusion. Choose the correct answer below. a. Since the p-value is greater than the given value of alpha, there is sufficient evidence to reject H_0. b. Since the p-value is less than the given value of alpha, there is sufficient evidence to reject H_0. c. Since the p-value is less than the given value of alpha, there is insufficient evidence to reject H_0. d. Since the p-value is greater than the given value of alpha, there is insufficient evidence to reject H_0.

Answer 1

1)

`H_0: p_1-p_2=0\\\\H_a: p_1-p_2>0`

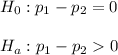
2) z=3.164

3) Critic value z₀=1.282.

4) P=0.00078

5) The correct answer is: "Since the p-value is less than the given value of alpha, there is sufficient evidence to reject H_0"

Explanation:

5.1) Being:

p₁: proportion of men who keep track of the deadlines in their head

p₂: proportion of women who keep track of the deadlines in their head

If we want to test if p₁ is larger than p₂, the null hypothesis and the alternative hypothesis should be:

`H_0: p_1-p_2=0\\\\H_a: p_1-p_2>0`

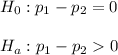
In this way, if we reject the null hypothesis, it can be claimed that p₁ is larger than p₂.

5.2) Compute the test statistic for the test.

First, we have to estimate a proportion as if the null hypothesis is true. This means the average of proportion of the samples taken from men and women, weighted by the sample size.

`\bar p=(n_1p_1+n_2p_2)/(n_1+n_2)=(500*0.54+500*0.44)/(500+500)= 0.49`

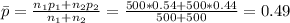
Then, we used this average to estimate the standard error

`s=\sqrt{(p(1-p))/(n_1)+{(p(1-p))/(n_2)}}=\sqrt{(0.49(1-0.49))/(500)+{(0.49(1-0.49))/(500)}}=√(0.0004998+0.0004998)\\\\s= 0.0316`

Lastly, we calculate the statistic z

`z=(p_1-p_2)/(s)=(0.54-0.44)/(0.0316)=(0.10)/(0.0316)=3.164`

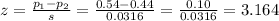
5.3) Give the rejection region for the test, using α = 0.10

For a one-tailed test with α = 0.10, the z value to limit the rejection region is z=1.282.

For every statistic larger than 1.282, the null hypothesis should be rejected.

5.4) Find the p-value for the test.

The p-value for a z=3.164 is P=0.00078 (corresponding to the area ot the standard normal distribution for a z larger than 3.164).

5.5) Choose the correct answer below.

The correct answer is: "Since the p-value is less than the given value of alpha, there is sufficient evidence to reject H_0"

The difference between the proportions is big enough to be statistically significant and enough evidence to reject the null hypothesis.