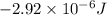This is an incomplete question, here is a complete question.
Two particles with charges +6 e⁻ and -10 e⁻ are initially very far apart (effectively an infinite distance apart). They are then fixed at positions that are 4.30 × 10⁻¹¹ m apart. What is EPE(final) - EPE(initial), which is the change in the electric potential energy?
Answer : The change in the electric potential energy is,
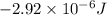
Explanation : Given,
Formula used for electric potential energy of the two charges when they are separated is:

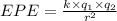
where,
EPE = electric potential energy
k =
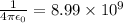
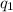 = charge on 1st particle = +6 e⁻ =
= charge on 1st particle = +6 e⁻ =
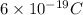
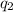 = charge on 2nd particle = -10 e⁻ =
= charge on 2nd particle = -10 e⁻ =
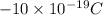
r = distance between two charges =
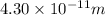
Now put all the given values in the above formula, we get:
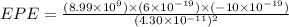

Initially EPE = 0 J
Thus,
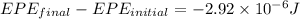
The positive sign indicate the attractive force and negative sign indicate the repulsive force.
Thus, the change in the electric potential energy is,