Step-by-step explanation:
It is known that the molecular weight of ammonia (
 ) is as follows.
) is as follows.
Molecular weight (
 ) =
) =
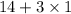 = 17
= 17
(a) Therefore, we will calculate the mass as follows.
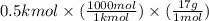
= 8500 g
Now, formula to calculate weight of the system in N is as follows.
Weight = mass × g
=
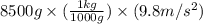
= 83.3 N (1
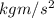 = 1 N)
= 1 N)
Hence, the weight of the system is 83.3 N.
(b) Relation between specific volume and number of moles is as follows.
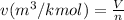
Therefore, calculate the specific volume as follows.
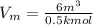
= 12
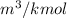
Also,
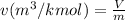
v =
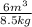
= 0.705882
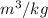
Therefore, we can conclude that the value of specific volume is 12
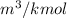 and 0.705882
and 0.705882
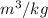 .
.