Answer:
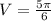 or 2.62
or 2.62
Explanation:
Since our region (on the left) is bounded by x = 1 and x = 0 (where
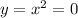 , if we take center at x = 2 then our radius will range from 1 to 2 (x=1 to x = 0). We can use the following integration to calculate the volume using shell method
, if we take center at x = 2 then our radius will range from 1 to 2 (x=1 to x = 0). We can use the following integration to calculate the volume using shell method
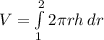
where r = 2 - x so x = 2 - r and
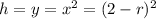 for
for
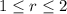
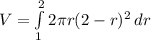
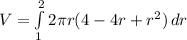

![V = 2\pi\left[(r^4)/(4) - (4r^3)/(3) + 2r^2\right]^2_1](https://img.qammunity.org/2021/formulas/mathematics/college/zfqfzheviup8m7jg12zfnb45p1so1u855w.png)
![V = 2\pi\left[\left((2^4)/(4) - (4*2^3)/(3) + 2*2^2\right) - \left((1^4)/(4) - (4*1^3)/(3) + 2*1^2\right)\right]](https://img.qammunity.org/2021/formulas/mathematics/college/2i0ihjp63rmnqqbemuh84rq7zmj6zehd67.png)
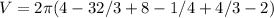
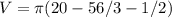
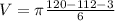
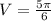 or 2.62
or 2.62