Question

A batch of 445 containers for frozen orange juice contains 3 that are defective. Two are selected, at random, without replacement from the batch. What is the probability that the second one selected is defective given that the first one was defective? Round your answer to five decimal places (e.g. 98.76543). What is the probability that both are defective? Round your answer to seven decimal places (e.g. 98.7654321). What is the probability that both are acceptable? (e.g. 98.765). Three containers are selected, at random, without replacement, from the batch. What is the probability that the third one selected is defective given that the first and second one selected were defective? (e.g. 98.765). What is the probability that the third one selected is defective given that the first one selected was defective and the second one selected was okay? Round your answer to five decimal places (e.g. 98.76543). What is the probability that all three are defective? (e.g. 98.765).

Answer 1

1. When Two containers are selected

(a) Probability that the second one selected is defective given that the first one was defective = 0.00450

(b) Probability that both are defective = 0.0112461

(c) Probability that both are acceptable = 0.986

2. When Three containers are selected

(a) Probability that the third one selected is defective given that the first and second one selected were defective = 0.002.

(b) Probability that the third one selected is defective given that the first one selected was defective and the second one selected was okay = 0.00451

(c) Probability that all three are defective = 6.855 x
`10^(-8)` .

Explanation:

We are given that a batch of 445 containers for frozen orange juice contains 3 defective ones i.e.

Total containers = 445

Defective ones = 3

Non - Defective ones = 442 { Acceptable ones}

• Two containers are selected, at random, without replacement from the batch.

(a) Probability that the second one selected is defective given that the first one was defective is given by;

Since we had selected one defective so for selecting second the available

containers are 444 and available defective ones are 2 because once

chosen they are not replaced.

Hence, Probability that the second one selected is defective given that the first one was defective =
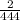`(2)/(444)` = 0.00450

(b) Probability that both are defective = P(first being defective) +

P(Second being defective)

=
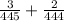`(3)/(445) + (2)/(444)` = 0.0112461

(c) Probability that both are acceptable = P(First acceptable) + P(Second acceptable)

Since, total number of acceptable containers are 442 and total containers are 445.

So, Required Probability =
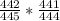`(442)/(445)*(441)/(444)` = 0.986

• Three containers are selected, at random, without replacement from the batch.

(a) Probability that the third one selected is defective given that the first and second one selected were defective is given by;

Since we had selected two defective containers so now for selecting third defective one, the available total containers are 443 and available defective container is 1 .

Therefore, Probability that the third one selected is defective given that the first and second one selected were defective =
`(1)/(443)` = 0.002.

(b) Probability that the third one selected is defective given that the first one selected was defective and the second one selected was okay is given by;

Since we had selected two containers so for selecting third container to be defective, the total containers available are 443 and available defective containers are 2 as one had been selected.

Hence, Required probability =
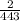`(2)/(443)` = 0.00451 .

(c) Probability that all three are defective = P(First being defective) +

P(Second being defective) + P(Third being defective)

=
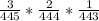`(3)/(445)* (2)/(444) * (1)/(443)` = 6.855 x
`10^(-8)` .