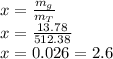Answer:
a) P = 2319.6[kPa]; b) 2.6%
Step-by-step explanation:
Since the problem data is not complete, the following information is entered:
A 1.78-m3 rigid tank contains steam at 220°C. One-third of the volume is in the liquid phase and the rest is in the vapor form. Determine (a) the pressure of the steam, and (b) the quality of the saturated mixture.
From the information provided in the problem we can say that you have a mixture of liquid and steam.
a) Using the steam tables we can see (attached image) that the saturation pressure at 220 °C is equal to:
![P_(sat) =2319.6[kPa]](https://img.qammunity.org/2021/formulas/physics/college/rosfxmub09juhc06qa9mj41apz6222kpc7.png)
![v_(f)=0.001190[m^(3)/hr]\\v_(g)=0.08609[m^(3)/hr]\\](https://img.qammunity.org/2021/formulas/physics/college/n93r4g7zmln3pycfpq4jkxjjumt52dbjq5.png)
b) Since the specific volume of the gas and liquid is known, we can find the mass of each phase using the following equation:
![m_(f)=(V_(f) )/(v_(f) ) \\m_(g)=(V_(g) )/(v_(g) ) \\where:\\V_(f)=volume of the fluid[m^3]\\v_(f)=specific volume of the fluid [m^3/kg]\\](https://img.qammunity.org/2021/formulas/physics/college/t0347sdpt1e84hqmjz5cj5ed6v2ybzacv5.png)
We know that the volume of the fluid is equal to:
![V_(f)=1/3*V_(total) \\V_(total)=1.78[m^3]\\](https://img.qammunity.org/2021/formulas/physics/college/atk6ly69r7smhziqyy1z785dk9w4vhgmbb.png)
Now we can find the mass of the gas and the liquid.
![m_(f)=(1/3*1.78)/(0.001190) \\m_(f)=498.6[kg]\\m_(g)=(2/3*1.78)/(0.08609)\\m_(g)=\ 13.78[kg]](https://img.qammunity.org/2021/formulas/physics/college/2gsy2ets7fdrfgd7l0ewvh4oj10fg6rbr5.png)
The total mass is the sum of both
![m_(total) =m_(g) + m_(fluid) \\m_(total) = 498.6 + 13.78\\m_(total) = 512.38[kg]](https://img.qammunity.org/2021/formulas/physics/college/a61z4gxy4c9wrkc3z2qpn9k9kfhe8n7h7q.png)
The quality will be equal to: