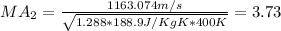Question

Determine the Mach number at the exit of the nozzle. The gas constant of carbon dioxide is R = 0.1889 kJ/kg·K. Take its constant pressure specific heat and specific heat ratio at room temperature to be cp = 0.8439 kJ/kg·K and k = 1.288.

Answer 1

To determine the Mach number at the exit of the nozzle, we can use the isentropic flow equations.

Step-by-step explanation:

To determine the Mach number at the exit of the nozzle, we need to use the isentropic flow equations. The Mach number (M) at the exit of the nozzle can be calculated using the equation:

M = sqrt( 2/(k-1) * ( (P/Pref) ^ ((k-1)/k) - 1) )

Where:

• k is the specific heat ratio (given as 1.288)
• P is the pressure at the exit of the nozzle
• Pref is the reference pressure (1 atm)

Given the information provided in the question, we can substitute the values into the equation to calculate the Mach number.

Answer 2

`MA_1 = \frac{50 m/s}{\sqtr{1.288*188.9 J/Kg K * 1200 K}}=0.093`

`MA_2 =(1163.074 m/s)/(√(1.288 *188.9 J/Kg K * 400 K))=3.73`

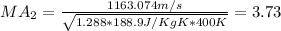
Step-by-step explanation:

Assuming this problem: "Carbon dioxide enters an adiabatic nozzle at 1200 K with a velocity of 50 m/s and leaves at 400 K. Assuming constant specific heats at room temperature, determine the Mach number (a) at the inlet and (b) at the exit of the nozzle. Assess the accuracy of the constant specific heat assumption."

Part a

For this case we can assume at the inlet we have the following properties:

`T_1 = 1200 K, v_1 = 50 m/s`

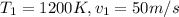
We can calculate the Mach number with the following formula:

`MA_1 = (v_1)/(c_1) = (v_1)/(√(kRT))`

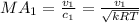
Where k represent the specific ratio given k =1.288 and R would be the universal gas constant for the carbon diaxide given by:
`R= 188.9 J/ Kg K`

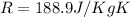
And if we replace we got:

`MA_1 = \frac{50 m/s}{\sqtr{1.288*188.9 J/Kg K * 1200 K}}=0.093`

Part b

For this case we can use the same formula:

`MA_2 = (v_2)/(c_2)`

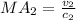
And we can obtain the value of v2 from the total energy of adiabatic flow process, given by this equation:

`c_p T_1 + (v^2_1)/(2)=c_p T_2 + (v^2_2)/(2)`

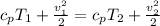
The value of
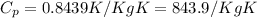`C_p = 0.8439 K /Kg K = 843.9 /Kg K` and the value fo T2 = 400 K so we can solve for
`v_2` and we got:

`v_2= √(2c_p (T_1 -T_2) +v^2_1)=1163.074 m/s`

And now we can replace on this equation:

`MA_2 = (v_2)/(c_2)`

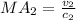
And we got:

`MA_2 =(1163.074 m/s)/(√(1.288 *188.9 J/Kg K * 400 K))=3.73`