The algebraic expression can be used to find the nth term of the sequence is:
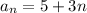
Where,
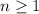 and n is a positive whole number
and n is a positive whole number
Solution:
Given sequence is:
8, 11, 14, 17, 20, 23
Let us find the common difference between terms
11 - 8 = 3
14 - 11 = 3
17 - 14 = 3
20 - 17 = 3
23 - 20 = 3
Thus the common difference between successive term and previous term is constant
Thus this is a arithmetic sequence
The formula for nth term term of arithmetic sequence is given as:

Where,
 is the nth term of sequence
is the nth term of sequence
 is the first term of sequence
is the first term of sequence
d is the common difference between terms
Here in this sequence, 8, 11, 14, 17, 20, 23
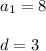
Therefore,
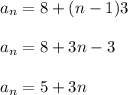
Where,
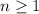 and n is a positive whole number
and n is a positive whole number
Thus algebraic expression can be used to find the nth term of the sequence is found