Question

A ½ in diameter rod of 5 in length is being considered as part of a mechanical

linkage in which it can experience a tensile loading and unloading during application. The
material being considered is a standard aluminum bronze with a Young’s modulus of 15.5 Msi.
What is the maximum load the rod can take before it starts to permanently elongate?
Considering the rod is designed so that it does not yield, what is the maximum energy that the
rod would store? [Hint: You can look up some properties of aluminum bronze in your machine
design book].

Answer 1

The maximum load the rod can take before it starts to permanently elongate = = 6086.84 lbf or 27075.59 N

The maximum energy that the rod would store =2.536 ft·lbf or 3.439 J

Step-by-step explanation:

We list out the variables to the question as follows

Rod diameter = 0.5 in

Length of rod = 5 in

Young's modulus of elasticity for the material = 15.5 Msi

The maximum load rthe rd can take before it starts to permanently elongate is the yield stress and it can vbe calclulated by applyng the 0.2% offset rule by taking the yeild strain to be equal to 2%

Thus Young's Modulus at yield point =
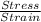`(Stress)/(Strain)` so that the yield stess is

Yield stress = strain × Young's Modulus

= 2/100 × E = 0.002 × 15.5 Msi = 0.031 Msi = 31 ksi

The maximum load that the rod would take before it starts to permanently elongate = F = Stress×Area

where area = π·D²/4 = 0.196 in²

F = 31 kSi × 0.196 in² = 6086.84 lbf or 27075.59 N

To calculate the strain energy stored in the rod we apply the strain energy formula thus

U = V×σ²/2·E

To calculate the volume we have V = L ×π·D²/4 =5 in × 0.196 in² = 0.98 in³

then U = 0.98 × (31000)²/(2·15.5×10⁶)

= 30.43 in³·psi = 2.536 ft·lbf

or 3.439 J

The maximum energy that the rod would store = 2.536 ft·lbf