Question

The car travels along the circular path such that its speed is increased by at = (0.5et ) m/s2 , where t is in seconds. Determine the magnitudes of its velocity and acceleration after the car has traveled s =18 m starting from rest. Neglect the size of the carDetermine the magnitude of its acceleration after the car has traveled s = 18 m starting from rest

Answer 1

acceleration = 24.23 ms⁻¹

Step-by-step explanation:

Let's gather the data:

The acceleration of the car is given by a = 0.5
`e^(t)`

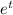
The acceleration is the change in the speed in relation to time. In other words:

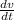`(dv)/(dt)` = a = a = 0.5
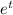`e^(t)` ...1

Solving the differential equation yields:

v = 0.5
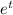`e^(t)` + C₁

Initial conditions : 0 = 0.5
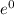`e^(0)` + C₁

C₁ = -5

at any time t, the velocity is: v= 0.5
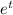`e^(t)`- 5

Solving for distance, s = 0. 5
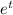`e^(t)` - 0.5 t - 0.5

18 = 0.5
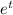`e^(t)` - 0.5 t - 0.5

t = 3.71 s

Substitute t = 3.71 s

v= 0.5
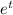`e^(t)`- 5

= 19.85 m/s

a = 0.5
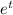`e^(t)` ...1

= 20.3531

an =
`(v^(2) )/(p)`

=
`((19.853)^(2) )/(30)`

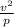
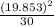
= 13.1382

Magnitude of acceleration =
`\sqrt{ (a)^(2) + (an)^(2) }`

=
`\sqrt{(20.3531)^(2) +(13.1382)^(2) }`

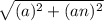
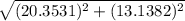
= 24.23 ms⁻¹ Ans