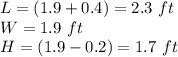Question

The dimensions of a portable kennel can be expressed as width x, length x + 0.4, and height x − 0.2? What are the dimensions of a portable kennel with a volume of 7.4 ft3? Use a graphing calculator to solve. Round the dimensions to the nearest tenth.

Answer 1

`L=2.3\ ft\\W=1.9\ ft\\H=1.7\ ft`

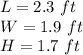
Explanation:

we know that

The volume of a portable kennel (rectangular prism) is equal to

`V=LWH`

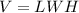
where

`L=(x+0.4)\ ft\\W=x\ ft\\H=(x-0.2)\ ft`

`V=7.4\ ft^3`

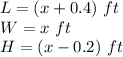
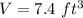
substitute the given values in the formula of volume

`7.4=(x+0.4)(x)(x-0.2)`

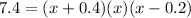
Apply distributive property right side

`7.4=x(x^2-0.2x+0.4x-0.08)`

`7.4=x(x^2+0.2x-0.08)`

`7.4=x^3+0.2x^2-0.08x`

`x^3+0.2x^2-0.08x-7.4=0`

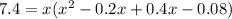
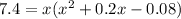
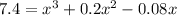
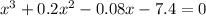
Solve the cubic equation by graphing

using a graphing tool

The solution is x=1.9

see the attached figure

Find the dimensions

substitute the value of x

`L=(1.9+0.4)=2.3\ ft\\W=1.9\ ft\\H=(1.9-0.2)=1.7\ ft`