Answer:
(a) 0.4096
(b) 0.64
(c) 0.7942
Step-by-step explanation:
The probability that the player wins is,
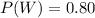
Then the probability that the player losses is,
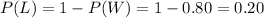
The player is playing the video game with 4 different opponents.
It is provided that when the player is defeated by an opponent the game ends.
All the possible ways the player can win is: {L, WL, WWL, WWWL and WWWW)
(a)
The results from all the 4 opponents are independent, i.e. the result of a game played with one opponent is unaffected by the result of the game played with another opponent.
The probability that the player defeats all four opponents in a game is,
P (Player defeats all 4 opponents) =
![P(W)* P(W)* P(W)* P(W)=[P(W)]^(4) =(0.80)^(4)=0.4096](https://img.qammunity.org/2021/formulas/mathematics/high-school/cfh4vpjmcstl60yty0acxcidquyl7fwig5.png)
Thus, the probability that the player defeats all four opponents in a game is 0.4096.
(b)
The probability that the player defeats at least two opponents in a game is,
P (Player defeats at least 2) = 1 - P (Player losses the 1st game) - P (Player losses the 2nd game) =

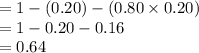
Thus, the probability that the player defeats at least two opponents in a game is 0.64.
(c)
Let X = number of times the player defeats all 4 opponents.
The probability that the player defeats all four opponents in a game is,
P(WWWW) = 0.4096.
Then the random variable
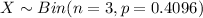
The probability distribution of binomial is:
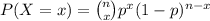
The probability that the player defeats all the 4 opponents at least once is,
P (X ≥ 1) = 1 - P (X < 1)
= 1 - P (X = 0)
![=1-[{3\choose 0}(0.4096)^(0) (1-0.4096)^(3-0)]\\=1-[1*1* (0.5904)^(3)\\=1-0.2058\\=0.7942](https://img.qammunity.org/2021/formulas/mathematics/high-school/eohxe111ap2k2u1pweskqxum0r84rw3alt.png)
Thus, the probability that the player defeats all the 4 opponents at least once is 0.7942.