Question

A player of a video game is confronted with a series of four opponents and an 80% probability of defeating each opponent. Assume that the results from opponents are independent (and that when the player is defeated by an opponent the game ends).

A. What is the probability that a player defeats all four opponents in a game?
B. What is the probability that a player defeats at least two opponents in a game?
C. If the game is played three times, what is the probability that the player defeats all four opponents at least once?

Answer 1

The probability of defeating all four opponents in one game is 40.96%. The probability of defeating at least two opponents is 87.04%. Playing the game three times, the probability of defeating all four opponents at least once is 88.47%.

Step-by-step explanation:

To calculate the probability of different outcomes when playing a video game against four opponents, we'll use basic probability rules and assumptions given in the question.

A. Probability of Defeating All Four Opponents

The probability of defeating each opponent is 80% or 0.8. Since the fights are independent, to find the probability of defeating all four, we multiply the probabilities together:
0.8 × 0.8 × 0.8 × 0.8 = 0.4096 or 40.96% chance of defeating all four opponents.

B. Probability of Defeating At Least Two Opponents

To find the probability of defeating at least two opponents, we must consider all possible combinations of winning 2, 3, or 4 opponents' fights, and add those probabilities together. Let W represent a win and L represent a loss:

• P(WWLL) + P(WLWL) + P(WLLW) + P(LWWL) + P(LWLW) + P(LLWW)
  
• P(WWWL) + P(WLWW) + P(WWLW) + P(LWWW)
  
• P(WWWW)
  

We already calculated P(WWWW) as 0.4096. The other probabilities can be calculated using similar multiplication of respective individual probabilities (0.8 for W, 0.2 for L). After calculation, we sum these to find the cumulative probability, which is 0.8704 or 87.04%.

C. Probability of Defeating All Four Opponents At Least Once Over Three Games:

The probability of not defeating all four opponents in one game is 1 - P(WWWW) = 0.5904. The events in each game are independent, so the probability of not defeating all four opponents in all three games is (0.5904)^3. Therefore, by subtracting this result from 1, we get the probability of defeating all opponents at least once: 1 - (0.5904 × 0.5904 × 0.5904) = 0.8847 or 88.47%.

Answer 2

(a) 0.4096

(b) 0.64

(c) 0.7942

Step-by-step explanation:

The probability that the player wins is,

`P(W)=0.80`

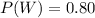
Then the probability that the player losses is,

`P(L)=1-P(W)=1-0.80=0.20`

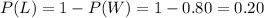
The player is playing the video game with 4 different opponents.

It is provided that when the player is defeated by an opponent the game ends.

All the possible ways the player can win is: {L, WL, WWL, WWWL and WWWW)

(a)

The results from all the 4 opponents are independent, i.e. the result of a game played with one opponent is unaffected by the result of the game played with another opponent.

The probability that the player defeats all four opponents in a game is,

P (Player defeats all 4 opponents) =
`P(W)* P(W)* P(W)* P(W)=[P(W)]^(4) =(0.80)^(4)=0.4096`

Thus, the probability that the player defeats all four opponents in a game is 0.4096.

(b)

The probability that the player defeats at least two opponents in a game is,

P (Player defeats at least 2) = 1 - P (Player losses the 1st game) - P (Player losses the 2nd game) =
`1-P(L)-P(WL)`

`=1-(0.20)-(0.80*0.20)\\=1-0.20-0.16\\=0.64`

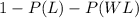
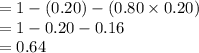
Thus, the probability that the player defeats at least two opponents in a game is 0.64.

(c)

Let X = number of times the player defeats all 4 opponents.

The probability that the player defeats all four opponents in a game is,

P(WWWW) = 0.4096.

Then the random variable
`X\sim Bin(n=3, p=0.4096)`

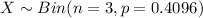
The probability distribution of binomial is:

`P(X=x)={n\choose x}p^(x) (1-p)^(n-x)`

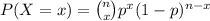
The probability that the player defeats all the 4 opponents at least once is,

P (X ≥ 1) = 1 - P (X < 1)

= 1 - P (X = 0)

`=1-[{3\choose 0}(0.4096)^(0) (1-0.4096)^(3-0)]\\=1-[1*1* (0.5904)^(3)\\=1-0.2058\\=0.7942`

Thus, the probability that the player defeats all the 4 opponents at least once is 0.7942.