Answer: The length of the shorter side of a golden rectangle is about 24.7 inches.
Explanation:
Given : A golden rectangle has side lengths in the ratio of about 1 to 1.62.
Since 1.62 > 1 , so
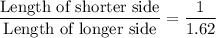
If the length of the longer side is 40 inches , then we have
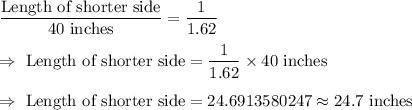
Hence, the length of the shorter side of a golden rectangle is about 24.7 inches.