Answer: a) 12.9 m b) 0.40 rad/s² c) 335.4 J d) 1349.06 J
Step-by-step explanation:
a)
Distance traveled= R∅
where ∅=
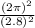 / 2*α
/ 2*α
To find α we have
Sum of torque= Iα
F x r x number of children = m*r²/2 * α
26 x
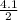 * 4 = (255) * (4.10/2)² /2 *α
* 4 = (255) * (4.10/2)² /2 *α
Solving we get,
α=
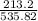
α= 0.40
So,
∅=
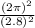 / 2*α
/ 2*α
Becomes
∅= 6.29
Now,
Distance traveled= 4.1/2 * 6.29
Distance traveled= 12.9 m
b)
Angular acceleration= 0.40
c)
Work done= F x distance traveled
Work done= 26 x 12.9
Work done= 335.4 J
d)
Kinetic energy=
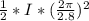
Putting values we get,
Kinetic energy= 267.91 * 5.03
Kinetic energy= 1349.06 J