Question

A man stands on the roof of a building of height 14.0 m and throws a rock with a velocity of magnitude 26.0 m/s at an angle of 28.0 ∘ above the horizontal. You can ignore air resistance.

Answer 1

The maximum height above the roof that the rock reaches is 7.6 meters.

Step-by-step explanation:

Given that, a man stands on the roof of a building of height 14.0 m and throws a rock with a velocity of magnitude 26.0 m/s at an angle of 28 degrees above the horizontal.

It is assumed to find the maximum height above the roof that the rock reaches. Let it is given by y. So,

`v^2-u^2=2ay`

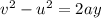
At maximum height, v = 0

Here, a = -g

`-(u\ sin\theta)^2=-2gy`

`(u\ sin\theta)^2=2gy`

`y=((u\ sin\theta)^2)/(2g)`

`y=((26* \ sin(28))^2)/(2* 9.8)`

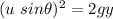
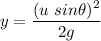
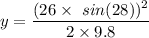
y = 7.60 meters

So, the maximum height above the roof that the rock reaches is 7.6 meters. Hence, this is the required solution.