Question

Calculate the sample standard deviation and sample variance for the following frequency distribution of heart rates for a sample of American adults. If necessary. round to one more decimal place than the largest number of decimal places given in the data. Heart Rates in Beats per Minute Class Frequency 61-6613 67-72 10 73-78 3 79-8411 85-90 3

Answer 1

`\bar X = (\sum_(i=1)^5 x_i f_i)/(n) = (2906)/(40)= 72.65`

`s^2 = (213856 -(2906)/(40))/(40-1)=70.131`

`s = √(70.131)= 8.374`

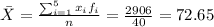
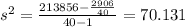
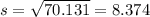
Explanation:

For this case we can calculate the expected value with the following table"

Class Midpoint(xi) Freq. (fi) xi fi xi^2 * fi

61-66 63.5 13 825.5 52419.5

67-72 69.5 10 695 48302.5

73-78 75.5 3 226.5 17100.75

79-84 81.5 11 896.5 73064.75

85-90 87.5 3 262.5 22968.75

________________________________________________

Total 40 2906 213856

For this case the midpoint is calculated as the average between the minimum and maximum point for each class.

The expected value can be calculated with the following formula:

`\bar X = (\sum_(i=1)^5 x_i f_i)/(n) = (2906)/(40)= 72.65`

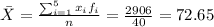
For this case n =40 represent the total number of obervations given,

And for the sample variance we can use the following formula:

`s^2 = (\sum x^2_i f_i -(\sum x_i f_i)/(n))/(n-1)`

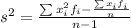
And if we replace we got:

`s^2 = (213856 -(2906)/(40))/(40-1)=70.131`

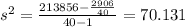
And for the deviation we take the square root:

`s = √(70.131)= 8.374`