Answer with Step-by-step explanation:
We are given that
DE
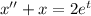
Function:

We have to show that given function is a solution of the equation for all values of the constants.
If given function is solution of DE then it satisfied the given DE.
Differentiate function w.r.t.t

Again differentiate w.r.t. t
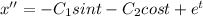
Substitute the values in the given DE
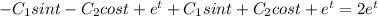
LHS=RHS
Given function satisfied the given DE.Therefore, it is solution of given DE for all values of the constants.