Answer:
The first possible value of d is 0.85 m
The second possible value of d is 2.55 m
The third possible value of d is 4.25 m
Step-by-step explanation:
Given that,
Distance =d
Frequency of sound wave= 200 Hz
We need to calculate the wavelength
Using formula of wavelength
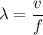
Put the value into the formula
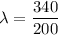
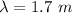
The separation between the speakers in the destructive interference is
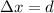
The equation for destructive interference
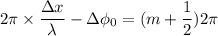
The loudspeakers are in phase
So,
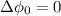
The equation for destructive interference is
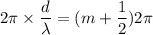 ....(I)
....(I)
Here, m = 0,1,2,3.....
We need to calculate the first possible value of d
For, m = 0
Put the value in the equation (I)
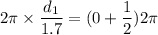
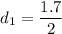
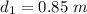
We need to calculate the second possible value of d
For, m = 1
Put the value in the equation (I)
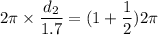
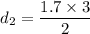
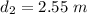
We need to calculate the third possible value of d
For, m = 1
Put the value in the equation (I)
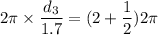
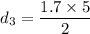
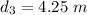
Hence, The first possible value of d is 0.85 m
The second possible value of d is 2.55 m
The third possible value of d is 4.25 m