Question

Two identical loudspeakers separated by distance dd emit 200 Hz sound waves along the x-axis. As you walk along the axis, away from the speakers, you don't hear anything even though both speakers are on.

What are the three lowest possible values of d? Assume a sound speed of 340 m/s.

Answer 1

The first possible value of d is 0.85 m

The second possible value of d is 2.55 m

The third possible value of d is 4.25 m

Step-by-step explanation:

Given that,

Distance =d

Frequency of sound wave= 200 Hz

We need to calculate the wavelength

Using formula of wavelength

`\lambda=(v)/(f)`

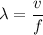
Put the value into the formula

`\lambda=(340)/(200)`

`\lambda=1.7\ m`

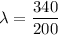
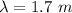
The separation between the speakers in the destructive interference is

`\Delta x= d`

The equation for destructive interference

`2\pi*(\Delta x)/(\lambda)-\Delta\phi_(0)=(m+(1)/(2))2\pi`

The loudspeakers are in phase

So,
`\Delta\phi_(0)=0`

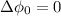
The equation for destructive interference is

`2\pi*(d)/(\lambda)=(m+(1)/(2))2\pi`....(I)

Here, m = 0,1,2,3.....

We need to calculate the first possible value of d

For, m = 0

Put the value in the equation (I)

`2\pi*(d_(1))/(1.7)=(0+(1)/(2))2\pi`

`d_(1)=(1.7)/(2)`

`d_(1)=0.85\ m`

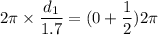
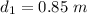
We need to calculate the second possible value of d

For, m = 1

Put the value in the equation (I)

`2\pi*(d_(2))/(1.7)=(1+(1)/(2))2\pi`

`d_(2)=(1.7*3)/(2)`

`d_(2)=2.55\ m`

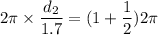
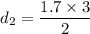
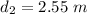
We need to calculate the third possible value of d

For, m = 1

Put the value in the equation (I)

`2\pi*(d_(3))/(1.7)=(2+(1)/(2))2\pi`

`d_(3)=(1.7*5)/(2)`

`d_(3)=4.25\ m`

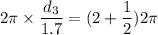
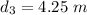
Hence, The first possible value of d is 0.85 m

The second possible value of d is 2.55 m

The third possible value of d is 4.25 m