Question

The product of a non-zero rational number and an irrational number can always be

Answer 1

The product of a non-zero rational number and an irrational number will always be an irrational number.

Explanation:

Here's a proof by contradiction for this claim.

Consider an irrational number
`x`. Assume by contradiction that this claim isn't true. In other words, assume that there exist a non-zero rational number
`y` such that
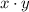`x \cdot y` is a rational number.

By the definition of rational numbers, a number is a rational number if and only if it can be written as the quotient of two integers.

• 
  `y` is a rational number ⇔ there exist two integers
  `a` and
  `b` such that
  `\displaystyle y = (a)/(b)`.
• 
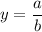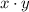  `x \cdot y` is a rational number ⇔ there exist two (other) integers
  `c` and
  `d` such that
  `\displaystyle x \cdot y = (c)/(d)`.

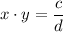Divide
`y` from both sides of the equation:

`\displaystyle (x\cdot y)/(y) = \left.(c)/(d)\right/y`.

The left-hand side of this equation is now equal to
`x`.

Since
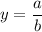`\displaystyle y = (a)/(b)` by assumption, the
`y` on the right-hand side of this equation can be replaced with
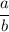`\displaystyle (a)/(b)`. Hence, the right-hand side of this equation would become

`\displaystyle (x\cdot y)/(y) = \left.(c)/(d)\right/(a)/(b) = (c)/(d)\cdot \left((b)/(a)\right) = (b \cdot c)/(a \cdot d)`.

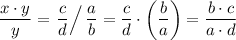Combine the two sides of the equation to obtain:

`x = \displaystyle (b \cdot c)/(a \cdot d)`.

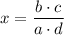Since
`b` and
`c` are both integers, their product
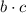`b \cdot c` would also be an integer. Similarly, since
`a` and
`d` are both integers, their product
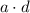`a \cdot d` would also be an integer.

In other words,
`x` can now be represented as the quotient of two integers. By the definition of rational numbers,

Hence, the original assumption that this claim isn't true, is not true. That verifies the claim that the product of a non-zero rational number and an irrational number would be an irrational number.