Answer:
The product of a non-zero rational number and an irrational number will always be an irrational number.
Explanation:
Here's a proof by contradiction for this claim.
Consider an irrational number
 . Assume by contradiction that this claim isn't true. In other words, assume that there exist a non-zero rational number
. Assume by contradiction that this claim isn't true. In other words, assume that there exist a non-zero rational number
 such that
such that
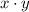 is a rational number.
is a rational number.
By the definition of rational numbers, a number is a rational number if and only if it can be written as the quotient of two integers.
 is a rational number ⇔ there exist two integers
is a rational number ⇔ there exist two integers
 and
and
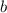 such that
such that
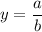 .
.
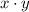 is a rational number ⇔ there exist two (other) integers
is a rational number ⇔ there exist two (other) integers
 and
and
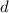 such that
such that
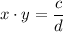 .
.
Divide
 from both sides of the equation:
from both sides of the equation:
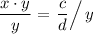 .
.
The left-hand side of this equation is now equal to
 .
.
Since
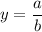 by assumption, the
by assumption, the
 on the right-hand side of this equation can be replaced with
on the right-hand side of this equation can be replaced with
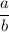 . Hence, the right-hand side of this equation would become
. Hence, the right-hand side of this equation would become
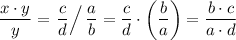 .
.
Combine the two sides of the equation to obtain:
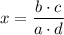 .
.
Since
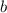 and
and
 are both integers, their product
are both integers, their product
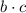 would also be an integer. Similarly, since
would also be an integer. Similarly, since
 and
and
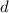 are both integers, their product
are both integers, their product
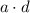 would also be an integer.
would also be an integer.
In other words,
 can now be represented as the quotient of two integers. By the definition of rational numbers,
can now be represented as the quotient of two integers. By the definition of rational numbers,
Hence, the original assumption that this claim isn't true, is not true. That verifies the claim that the product of a non-zero rational number and an irrational number would be an irrational number.