Answer:
(a) the pressure and temperature at the end of the heat addition process is 1733.79 K and 4392.26 Kpa respectively
(b) the net work output is 423.54 KJ/Kg
(c) the thermal efficiency is 56.5%
(d) the mean effective pressure for the cycle cannot be determined without initial volume of the process
Step-by-step explanation:
Assumptions:
- changes in kinetic and potential energy is negligible
- air is an ideal gas with constant specific heats
The properties of air at room temperature;
Cp = 1.005 KJ/kg.K, Cv = 0.718KJ/kg.K, R = 0.287KJ/kg.K and K = 1.4
Part a:
For isentropic compression:
![T_2=T_1[(V_1)/(V_2)]^(K-1)](https://img.qammunity.org/2021/formulas/engineering/college/hlxoohe57kokxocilo5t0c66923tenf2bs.png)
Where;
T₁ = (27+273)K =300K
V₁/V₂ = 8
![T_2=300[8]^(1.4-1) = 300[8]^(0.4) = 689.22K](https://img.qammunity.org/2021/formulas/engineering/college/nkhy0aob5yppeky7ztlrilzkmd0f1lpc4g.png)
Based on the assumption above;
Q₁ₙ = U₃ -U₂
For an ideal gas with constant specific heats, the change in internal energy in terms of the change in temperature is shown below
U₃ -U₂ = Cv(T₃-T₂)
Thus; Q₁ₙ = Cv(T₃-T₂)
T₃ = (Q₁ₙ/Cv) + T₂
T₃ = (750/0.718) + 689.22 K = 1733.79 K
From general gas equation, we find the second stage pressure
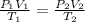
![P_2 =P_1[(T_2)/(T_1)][(V_1)/(V_2)] = 95 Kpa[(689.22)/(300)](8)](https://img.qammunity.org/2021/formulas/engineering/college/pdlxtd0b1ulyetfyygpf9vf2czscjferhp.png)
P₂ = 1746.024Kpa
To obtain the pressure at stage 3
![P_3 =P_2[(T_3)/(T_2)][(V_2)/(V_3)] = 1746.024 Kpa[(1733.79)/(689.22)](1)](https://img.qammunity.org/2021/formulas/engineering/college/1qgv0obhyb07jm54jtctjjajvj4vqssc1u.png)
P₃ = 4392.26 Kpa
Part b:
To obtain net work output we consider overall energy balance on the cycle
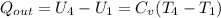
For is isentropic expansion
![T_4=T_3[(V_3)/(V_4)]^(K-1) = 1733.79 [(1)/(8)]^(0.4) = 754.68K](https://img.qammunity.org/2021/formulas/engineering/college/9iwslecx3eif0xr7v5zxf9x4yc9bczswy5.png)
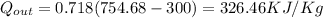
To solve for net work output:
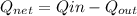 = (750 - 326.46) KJ/Kg = 423.54 KJ/Kg
= (750 - 326.46) KJ/Kg = 423.54 KJ/Kg
part c:
To calculate the thermal efficiency, we use net work output per input work
η = 423.54/750
η = 0.565 = 56.5%
part d:
Mean effective pressure for the cycle (MEP)
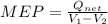 =
=
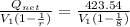
MEP =
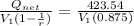
Thus mean effective pressure cannot be determined without initial volume of the process.