Question

A 3.0-kg block starts at rest at the top of a 37° incline, which is 5.0 m long. Its speed when it reaches the bottom is 2.0 m/s. What is the average friction force opposing its motion?

Answer 1

Answer:
`f_(r)` = 16.49N

Explanation: The object is placed on an inclined plane at an angle of 37° thus making it weight have two component,

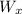`W_(x)` = horizontal component of the weight = mgsinФ

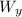`W_(y)` = vertical component of weight = mgcosФ

Due to the way the object is positioned, the horizontal component of force will accelerate the object thus acting as an applied force.

by using newton's law of motion, we have that

mgsinФ -
`f_(r)` = ma

where m = mass of object=5kg

a = acceleration= unknown

Ф = angle of inclination = 37°

g = acceleration due to gravity = 9.8
`m/s^(2)`

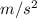
`f_(r)` = frictional force = unknown

we need to first get the acceleration before the frictional force which is gotten by using the equation below

`v^(2) = u^(2) + 2aS`

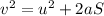
where v = final velocity = 2m/s

u = initial velocity = 0m/s (because the object started from rest)

a= unknown

S= distance covered = length of plane = 5m

`2^(2) = 0^(2) + 2*a*5\\\\4= 10 *a\\\\a = (4)/(10) \\a = 0.4m/s^(2)`

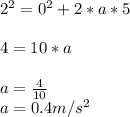
we slot in a into the equation below to get frictional force

mgsinФ -
`f_(r)` = ma

3 * 9.8 * sin 37 -
`f_(r)` = 3* 0.4

17.9633 -
`f_(r)` = 1.2

`f_(r)` = 17.9633 - 1.2

`f_(r)` = 16.49N