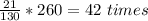Question

Sofia places 26 tiles representing each letter of the alphabet into a bag. Five of the tiles represent the vowels A, E, I, O, and U. Sofia will randomly select 1 tile from the bag and without replacement select another tile from the bag. Sofia will draw two tiles from the bag 260 times. What is a reasonable prediction for the number of times Sofia will select a consonant tile and a vowel tile?

Answer 1

42 times.

Explanation:

The number of total alphabet = 26 tiles

The number of vowels = 5

The number of consonant = 26 - 5 = 21

Sofia will randomly select 1 tile from the bag and without replacement select another tile from the bag.

The probability to select consonant at first time = 21/26

Total tiles after the first selection = 26 - 1 = 25

The probability to select vowels at second time = 5/25

The probability to select consonant and vowels =
`(21)/(26) *(5)/(25) =(21)/(130)`

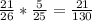
Sofia will draw two tiles from the bag 260 times.

The prediction for the number of times Sofia will select a consonant tile and a vowel tile =
`(21)/(130) *260=42 \ times`