Answer:
a) 740 W b) 6.2 A c) 8.1%
Step-by-step explanation:
We need first to get the total energy spent during the 30 days, that can be calculated as follows:
1 month = 30 days = 720 hr
If the total cost amounts $80 (for 720 hr), and the cost per kwh is 0.15, we have:
80 $/mo = 0.15 $/Kwh*x Kwh/mo
Solving for the total energy spent in the month:
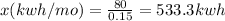
Assuming that the power delivered is constant over the entire 30 days, as power is the rate of change of energy, we can find the power as follows:
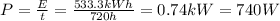
b) If the power is supplied by a voltage of 120 V, we can find the current I as follows:

c) If part of the electrical load is a 60-W light, we can substract this power from the one we have just found, as follows:
P = 740 W - 60 W = 680 W
The new value of the energy spent during the entire month will be as follows:
E = 0.68 kW*24(hr/day)*30(days/mo) = 490 kWh/mo
The reduction in percentage regarding the total energy spent can be calculated as follows:
ΔE =
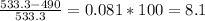
⇒ ΔE(%) = 8.1%
