Question

To treat a burn on his hand, a person decides to place an ice cube on the burned skin. The mass of the ice cube is 19.2 g, and its initial temperature is − 10.6 ∘ C. The water resulting from the melted ice reaches the temperature of his skin, 29.0 ∘ C. How much heat is absorbed by the ice cube and resulting water? Assume that all of the water remains in the hand.

Answer 1

Answer : The heat absorbed by the ice cube and resulting water is, 9.15 kJ

Solution :

The process involved in this problem are :

`(1):H_2O(s)(-10.6^oC)\rightarrow H_2O(s)(0^oC)\\\\(2):H_2O(s)(0^oC)\rightarrow H_2O(l)(0^oC)\\\\(3):H_2O(l)(0^oC)\rightarrow H_2O(l)(29.0^oC)`

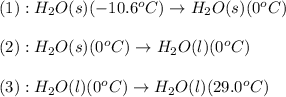
The expression used will be:

`\Delta H=[m* c_(p,s)* (T_(final)-T_(initial))]+m* \Delta H_(fusion)+[m* c_(p,l)* (T_(final)-T_(initial))]`

where,

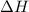`\Delta H` = heat available for the reaction =
`4.50* 10^3kJ=4.50* 10^6J`

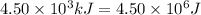
m = mass of ice = 19.2 g

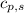`c_(p,s)` = specific heat of solid water or ice =
`2.01J/g^oC`

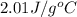
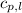`c_(p,l)` = specific heat of liquid water =
`4.18J/g^oC`

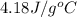
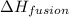`\Delta H_(fusion)` = enthalpy change for fusion =
`6.01kJ/mole=6010J/mole=(6010J/mole)/(18g/mole)J/g=333.89J/g`

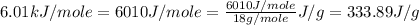
Molar mass of water = 18 g/mole

Now put all the given values in the above expression, we get:

`\Delta H=[19.2g* 2.01J/g^oC* (0-(-10.6))^oC]+19.2g* 333.89J/g+[19.2g* 4.18J/g^oC* (29.0-0)^oC]`

`\Delta H=9147.1872J=9.15kJ`

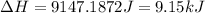
Therefore, the heat absorbed by the ice cube and resulting water is, 9.15 kJ