Answer:
The length of the shadow is increasing with the rate of 1.5 feet per sec
Explanation:
Let AB and CD represents the height of the lamppost and child respectively ( shown below )
Also, let E be a point represents the position of child.
In triangles ABE and CDE,
 ( right angles )
( right angles )
 ( common angles )
( common angles )
By AA similarity postulate,
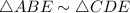
∵ Corresponding sides of similar triangles are in same proportion,
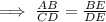
We have, AB = 12 ft, CD = 4 ft, BE = BD + DE = 6 + DE,
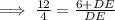
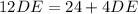
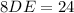
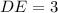
Now, the speed of walking = 2 mph =
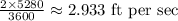
Note: 1 mile = 5280 ft, 1 hour = 3600 sec
Thus, the time taken by child to reach at E
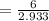
= 2.045 hours
Hence, the change rate in the length of shadow
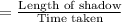

= 1.5 ft per sec.